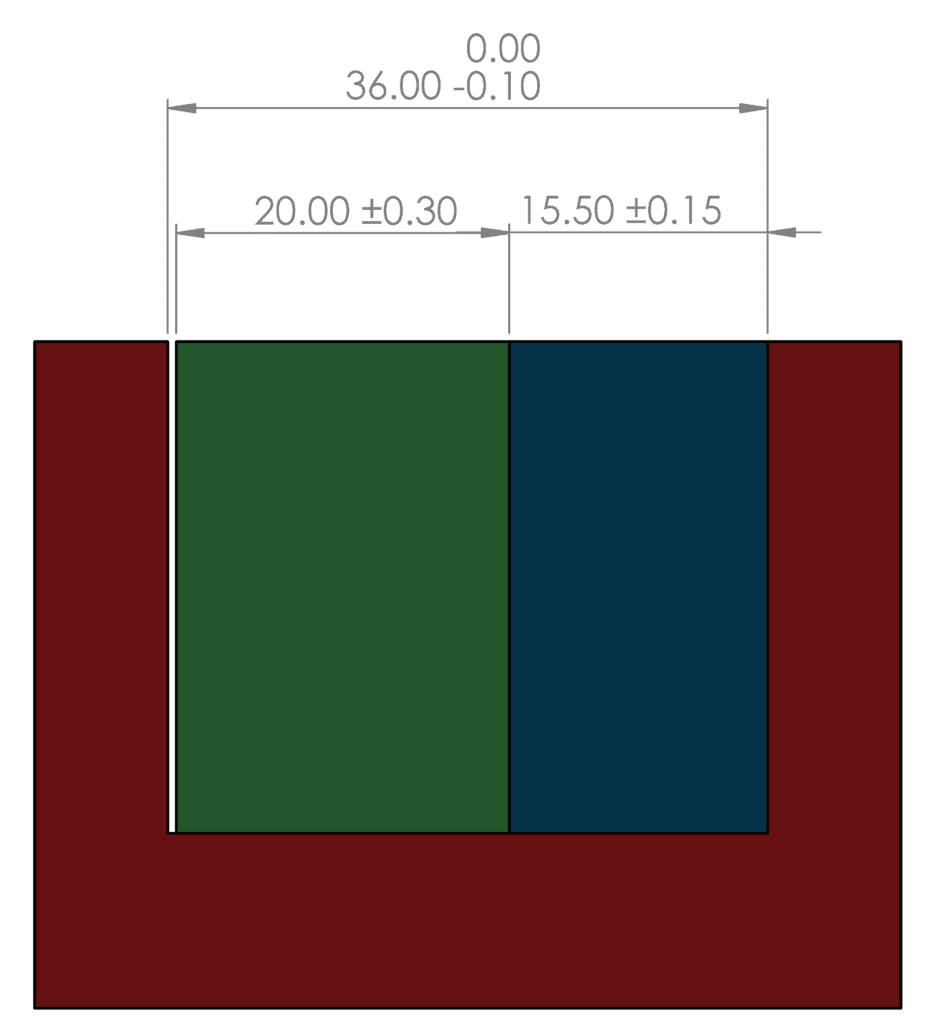
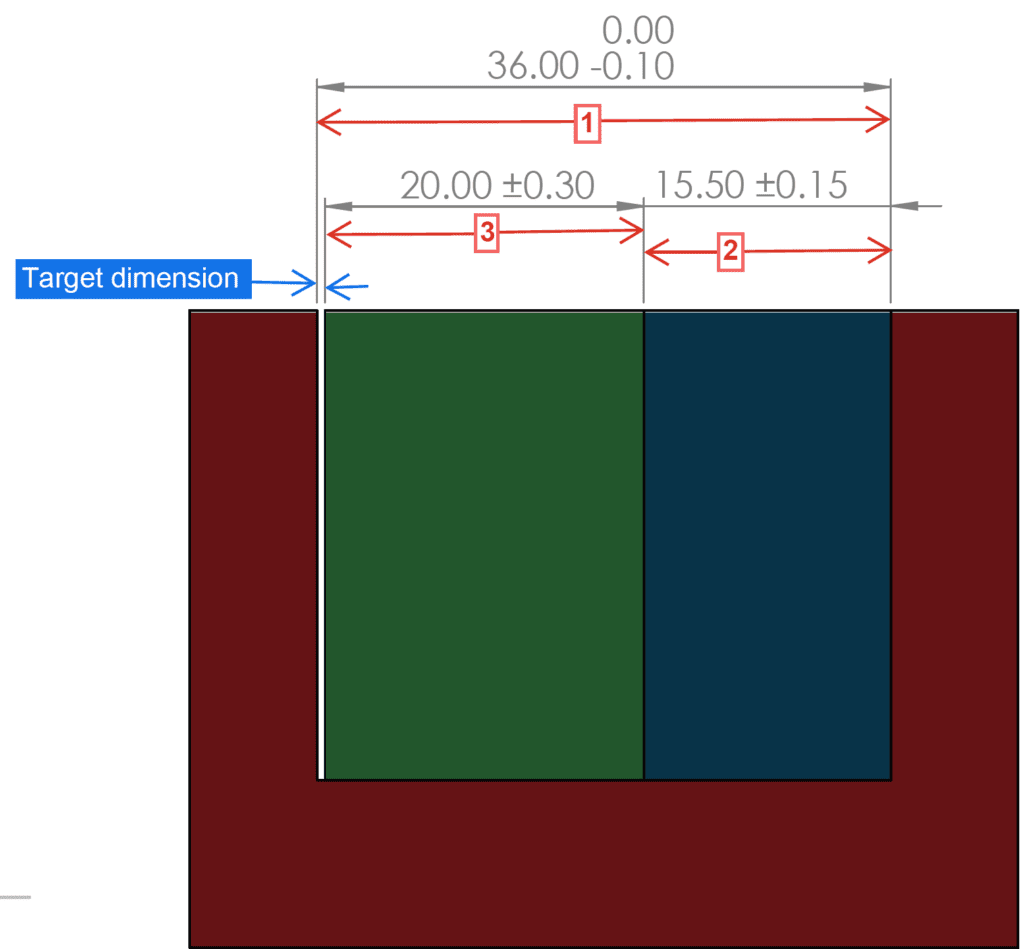
Identify the target dimension of interest. In this case, the clearance between the blocks and the pocket
Starting from one end of the target dimension, draw vectors through each relevant dimension, in order to create a loop so that you reach the other end of the target dimension. Assign a number to each vector.
Assign a positive direction. In this case positive will be towards the right, so that vector 1 will have a positive value, and vectors 2 and 3 will have negative values.
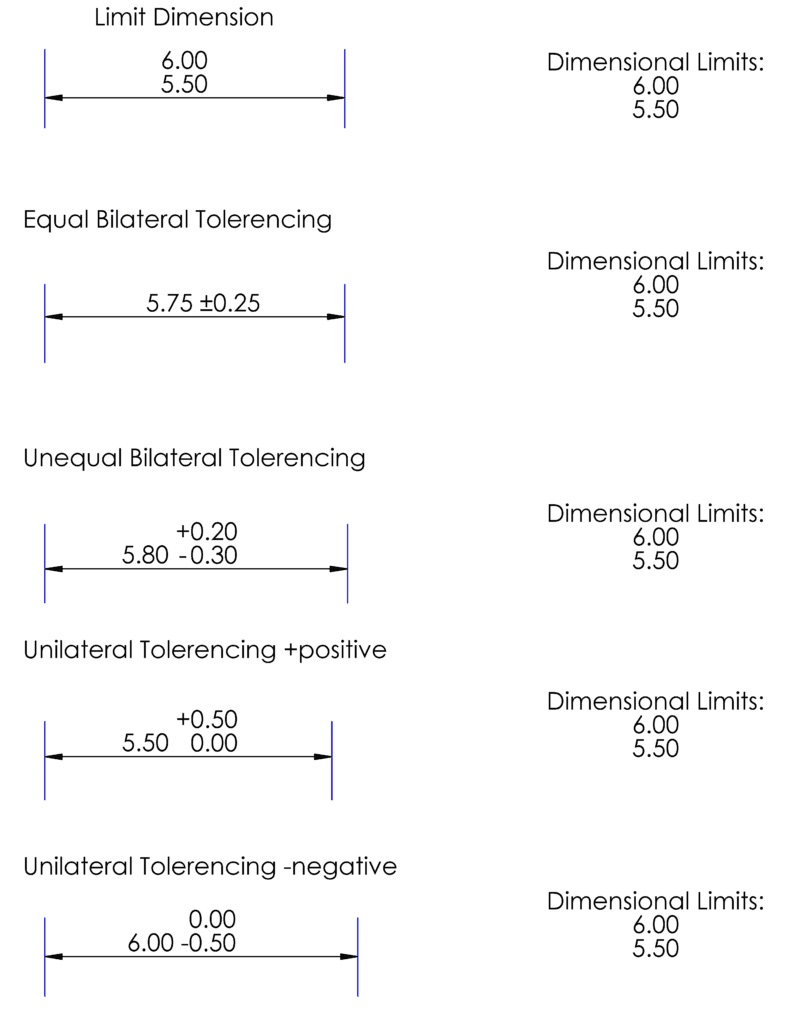
All tolerances must be symmetric bilateral. In this example, dimension 1 is given as unilateral. In order to convert it, we must center the nominal value and give it an equal bilateral tolerance. This results in:
Dimension1 : 35.95 ± 0.05
In the picture below you can find examples of different types of tolerance. For the purpose of tolerance analysis, all of these are equivalent and Equal Bilateral Tolerancing must be used.
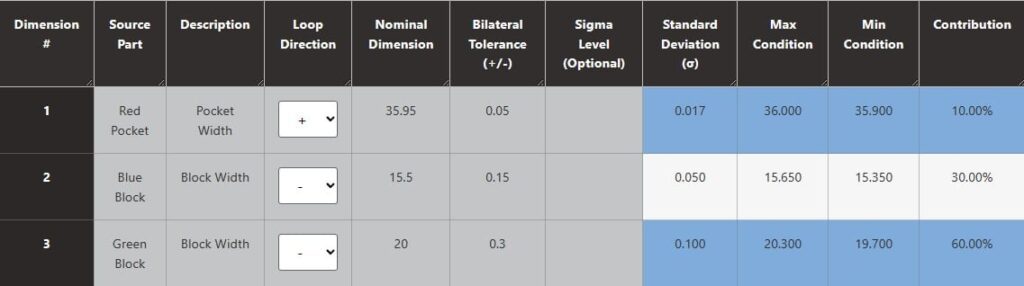
The ‘Nominal’ column shows the nominal value of the gap that we will have between the blocks and the pocket. Max and Min Condition show the extreme cases for each analysis type.
Worst Case scenario, as expected, predicts the largest range of variation. That is, under Max Condition, the clearance could be up to 0.95, however, under Min Conditions, there would be interference (blocks won’t fit in the pocket), as shown by the negative sign.
In order to understand what is more likely to happen, we need to make use of statistical analysis.
The calculator also does a Root Sum Square (RSS) type of analysis, which is essentially calculating a standard deviation for the assembly, thus creating a bilateral tolerance for the assembly: Toleranceassembly = ±3σassembly. This shows that in most cases both blocks will fit inside the pocket, and interference is not likely.
Additionally, the adjusted RSS analysis is performed. This analysis is more suitable for high-volume production processes where the mean value of a process may be shifted by 1.5σassembly

Note: To perform a meaningful RSS (Root Sum Square) stack-up tolerance analysis, some assumptions are made: Independent Variations, Normally Distributed Variations, and Tolerance Accumulation Linearity
© Me Vertuoso All Rights Reserved 2025